VIVIN ANGGRAINI HARDI: DETERMINAN MATRIKS

Pengertian Determinan Matriks

Determinan ialah sebuah nilai yang dapat di hitung dari unsur suatu matriks persegi. Determinan matriks A ditulis dengan tanda det( A ), det A, atau | A |. Determinan dapat di anggap sebagai faktor penskalaan transformasi yang digambarkan oleh matriks.

Sifat – Sifat Determinan Matriks

Ada beberapa sifat – sifat determinan matriks, yaitu diantarannya:

1. Apabila semua elemen dari salah satu baris atau kolom sama dengan nol, maka determinan matriks tersebut adalah nol. Perhatikan contoh berikut:

Misalkan : $A=\begin{bmatrix} 0 & 0\\ 2 & 3 \end{bmatrix}\rightarrow \left | A \right |=0;\: B=\begin{bmatrix} 2 & 3 & 1\\ 0 & 0 & 0\\ 5 & 4 & 1 \end{bmatrix}\rightarrow \left | B \right |=0$

2. Apabila semua elemen dari salah satu baris atau kolom itu sama dengan elemen-elemen baris atau kolom lain, maka determinan matriks tersebut adalah nol.

Perhatikan contoh berikut:

Misalkan: B = $\begin{bmatrix} 4 & 3 & 2\\ 5 & 7 & 8\\ 4 & 3 & 2 \end{bmatrix}\rightarrow \left | B \right |=0$ (Sebab elemen-elemen baris ke-1 dan ke-3 adalah sama).

3. Apabila elemen-elemen salah satu dari baris atau kolom adalah merupakan kelipatan dari elemen-elemen baris atau kolom lain maka determinan matriks tersebut adalah nol.

Perhatikan contoh di bawahberikut:

Misalkan: A = $\begin{bmatrix} 1 & 2 & 3\\ 5 & 7 & 0\\ 2 & 4 & 6 \end{bmatrix}\rightarrow \left | A \right |=0$ (Sebab elemen-elemen baris ke-3 sama dengan kelipatan elemen-elemen baris ke-1).

4. |AB| : |A| ×|B|

5. |AT| = |A|, untuk AT ialah transpose dari matriks A.

6. |A–1| = $\frac{1}{\left | A \right |}$ , untuk A–1 ialah invers dari matriks A.

7. |kA| = kn |A|, untuk A ordo n × n dan k adalahsuatu konstanta.

Determinan Matriks Ordo 2 x 2

Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.

$\textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix}$

Nilai determinan A disimbolkan dengan 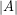$\left| A \right|$ , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.

$det(A) \; = \; \left| A \right| = ad - bc$

Determinan Matriks Ordo 3 x 3

Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.

$\textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$

Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.

Yang perlu dipahami ialah Determinan Utama, Determinan Variabel x dan Determinan Variabel y, penjelasannya seperti di bawah ini :

Determinan Utama ( D ) :

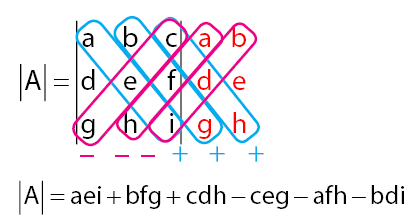
Determinan utama ialah sebuah determinan yang koefisiennya x dan y. Koefisien x masing – masing terletak pada kolom pertamanya, sedangkan koefisien y terletak masing – masing di kolom keduanya.

Determinan Variabel x ( Dx ) :

Determinan variabel x ialah sebuah determinan yang diperoleh dengan cara mengganti koefisien – koefisien variabel x dari determinan utama dengan bilangan- bilangan ruas sebelah kanannya.

Determinan Variabel y ( Dy ) :

Determinan variabel y ialah sebuah determinan yang diperoleh dengan cara mengganti koefisien – koefisien variabel y dari determinan utama dengan bilangan – bilangan ruas sebelah kanannya.

Contoh dan Pembahasan

Contoh 1