TEOREMA SISA

Misalkan suku banyak fx= a₂x²+a₁x+ a₀ dibagi dengan (x-k) memberikan hasil bagi H(x) dan sisa S, sehingga diperoleh hubungan : 

Keterangan:

f(x)   = suku banyak

(x-k)   = pembagi suku banyak

H(x)   = hasil bagi suku banyak

S(x)   = sisa suku banyak

Untuk menentukan hasil bagi H(x) dan sisa S digunakan pembagian suku banyak dengan cara pembagian bersusun berikut ini : 

Jadi, Hasil bagi H(x) = a₂x + a₂k + a₁ (pada bagian atas) dan sisa S (pada bagian bawah) = a₀+ a₁k + a₂k²

Poin yang harus diketahui dari Teorema Sisa

Contoh Soal dan Pembahasan

Contoh 1

Contoh 2

Contoh 3

Tentukan sisa hasil bagi 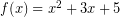 oleh .

 Pembahasan :

 Jika suku banyak f(x) berderajat n dibagi dengan , maka sisanya adalah S(x) = f(x).

Jadi, untuk mendapatkan sisa pembagian suku banyak, kita hanya perlu substitusi nilai k pada persamaan suku banyak.

  

Sekarang, susbtitusi nilai 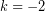 pada .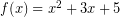

  

  

  

Berdasarkan teorema sisa dapat disimpulkan bahwa sisa hasil pembagian adalah 3. 

Contoh 4

Jika suku banyak f(x) = x⁴ + 3x³ + x² - (p + 1)x + 1 dibagi oleh (x - 2) sisanya adalah 35. Nilai p = .....

Pembahasan :

f(x) = x⁴ + 3x³ + x² - (p + 1)x + 1 dibagi oleh (x - 2), maka sisanya adalah f(2).
f(2) = (2)⁴ + 3(2)³ + (2)² - (p + 1)(2) + 1

f(2) = 16 + 24 + 4 - 2p - 2 + 1
f(2) = 43 - 2p
Karena sisa = f(2) = 35, maka:
43 - 2p = 35
<=> -2p = 35 - 43
<=> -2p = -8

<=> p = -8/-2
<=> p = 4

Contoh 5

Suku banyak 6x³ + 7x² + px - 24 habis dibagi oleh 2x - 3. Nilai p = .....

Pembahasan :

Misalkan f(x) = 6x³ + 7x² + px - 24

Karena f(x) habis dibagi oleh (2x - 3) maka sisa pembagiannya = f(32) = 0

f(32) =  6(32)³ + 7(32)² + p(32) - 24

f(32) = 6(278) + 7(94) + 3p2 - 24

f(32) = 1628 + 634 + 3p2 - 24

f(32) = 1628 + 1268 + 12p8 - 24

f(32) = 288+12p8 - 24

Karena f(32) = 0, maka:

288+12p8 - 24 = 0

<=> 288+12p8 = 24

<=> 288 + 12p = 24 x 8

<=> 288 + 12p = 192

<=> 12p = 192 - 288

<=> 12p = -96

<=> p = -96/12

<=> p = -8

Contoh 6

Fungsi f(x) dibagi (x - 1) sisanya 3, sedangkan jika dibagi (x - 2) sisanya 4. Jika dibagi x² - 3x + 2, maka sisanya adalah.....

Pembahasan :

f(x) dibagi (x - 1) sisanya 3, maka f(1) = 3

f(x) dibagi (x - 2) sisanya 4, maka f(2) = 4

Jika f(x) dibagi oleh x² - 3x + 2, maka diperoleh hasil H(x) dan sisa pembagiannya S(x). Sisa pembagian S(x) adalah berderajat 1.

Misalkan S(x) = px + q, maka:

f(x) = (x² - 3x + 2).H(x) + S(x)

f(x) = (x - 1)(x - 2).H(x) + (px + q)

Subtitusi nilai-nilai nol dari pembagi, yaitu x = 1 dan x = 2 ke persamaan f(x).

* Untuk x = 1

   f(1) = (1 - 1)(1 - 2).H(1) + (p(1) + q)
   <=> 3 = 0.(-1).H(1) + (p + q)
   <=> 3 = p + q ...............(1)

* Untuk x = 2
   f(2) = (2 - 1)(2 - 2).H(2) + (p(2) + q)
   <=> 4 = 1.0.H(2) + (2p + q)
   <=> 4 = 2p + q .............(2)

Eliminasi persamaan (1) dan (2), diperoleh:
  p + q = 3
2p + q = 4 -
<=> -p = -1
<=> p = 1

Subtitusi nilai p = 1 ke persamaan (1) diperoleh q = 2.
Jadi, sisa pembagiannya adalah x + 2.

Contoh 7

Carilah sisa pembagi suku banyak 8x³-2x²+5 dengan (x+2)

Pembahasan : 

a. Menggunakan substitusi

b. Menggunakan skema (bagan) dengan pembagian (x-k)

Jadi, sisanya S = f(-2) = -67 menggunakan teorema sisa. 

Contoh 8

Contoh 9 

Contoh 10