Soal-Soal tentang Pythagoras

1. Perhatikan gambar berikut

  Panjang sisi miringnya adalah ..

  Pembahasan :

  

2. Perhatikan gambar berikut

  tentukan panjang AC dari segitiga diatas
  Pembahasan :

3. Terdapat suatu segitiga siku-siku dengan ukuran dua sisi yang berpenyiku adalah 21 cm dan 28 cm. Tentukan panjang sisi yang lainnya.
Pembahasan :

4.  Suatu segitiga siku-siku KLM dengan siku-siku di L digambarkan seperti di bawah ini:

Tentukan panjang sisi KL pada gambar di atas!

pembahasan :

5. Terdapat segitiga siku-siku sama kaki dengan ukuran sisi miringnya adalah 5√2 cm. Tentukan panjang sisi yang lainnya.
Pembahasan :

6. Diketahui ukuran dua sisi yang berpenyiku dari segitiga siku-siku adalah 12 cm dan 16 cm. Tentukan ukuran sisi yang lainnya.

Pembahasan :

7. Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan seperti di bawah ini:

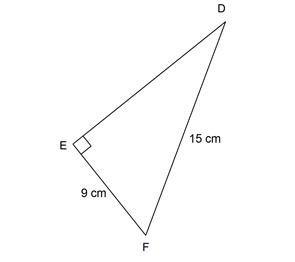
Tentukan panjang sisi DE pada gambar di atas!

Pembahasan :

8. Diketahui suatu bayangan menara memiliki panjang 10 m, jika jarak ujung menara dengan ujung bayangan menara adalah 26 m, tentukan tinggi menara tersebut.

Pembahasan :

9. Diketahui segitiga siku-siku ABC dengan siku-siku berada di B. Apabila panjang sisi AB = 16 cm serta Panjang sisi BC = 12 cm.

Maka hitunglah panjang sisi AC pada segitoga di atas!

Pembahasan :

Dari soal di atas bisa kiat gambarkan sebuah segitiga siku-siku seperti berikut ini:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini: 

10. Perhatikan baik-baik gambar di bawah ini:

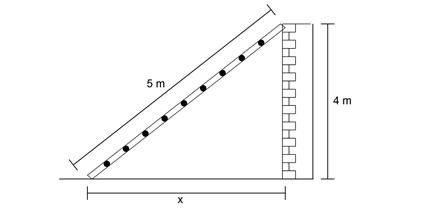
Diketahui suatu tangga disandarkan pada tembok. Apabila panjang tangga yaitu 5 m serta tinggi temboknya yaitu 4 m. Maka hitunglah jarak antara kaki tangga dengan temboknya!

Pembahasan:

Misalnya jarak antara kaki tangga dengan tembok yaitu x, maka untuk menentukan nilai x bisa kita pakai Rumus Phytagoras seperti berikut ini:

Diketahui:

• sisi miring atau c = 5m
• tinggi atau b = 4m

Ditanyakan:

• alas atau x?

x² = c²  – b² 

c² = 5² – 4² 

c² = 25 – 16 

c² = 9 

c = √9 

c = 3

11. Perhatikan baik-baik gambar di bawah ini:

Suatu kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 15 km menuju arah utara. Seudah tiba pada Pelabuhan B, kapal tersebut berlayar kembali sejauh 36 km menuju arah timur. Tentukan jarak antara pelabuhan A dengan titik akhir!

Pembahasan :

Dari soal di atas bisa kita bikin suatu gambar dengan informasi seperti yang terdapat pada penyelesaian di bawah ini:

Ditanyakan:

• sisi miring atau c

Diketahui:

• b = 36km
• a = 15km

Sehingga:

Jarak pelabuhan A ke titik akhir yaitu:

c² = 15²  + 36²
c² = 225 + 1296
c² = 1521
c = √1521
c = 39