SUDUT DAN GARIS

A. Pengertian Sudut

Sudut adalah istilah penting dan memiliki beberapa definisi yaitu Bentuknya dibuat dengan 2 garis lurus yang bertemu pada sebuah titik. Membuat sebuah jarak pada 2 garis tersebut.

B. Jenis-Jenis Sudut

jenis-jenis sudut berdasarkan besar sudutnya.

1. Sudut lancip

Perhatikan gambar berikut.

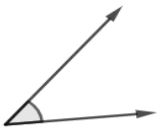
Sudut lancip merupakan jenis sudut dengan ukuran sudut antara 0° – 90° (kurang dari 90°).

2. Sudut siku-siku

Perhatikan gambar berikut.

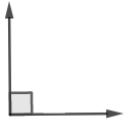
Pada gambar di atas terdapat sudut siku-siku. Sudut siku-siku memiliki besar sudut 90°.

3. Sudut tumpul

Perhatikan gambar berikut.

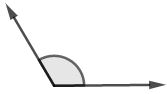
Sudut tumpul merupakan salah satu jenis sudut dengan ukuran sudut lebih dari 90° dan kurang dari 180°.

4. Sudut lurus

Perhatikan gambar berikut.

Gambar di atas merupakan sudut lurus dengan besar sudut 180°.

5. Sudut refleks

Perhatikan gambar berikut.

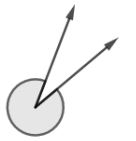
Gambar di atas merupakan gambar sudut refleks. Sudut refleks memiliki besar sudut lebih dari 180° dan kurang dari 360°.

C. Hubungan antara Sudut

Perhatikan gambar berikut.

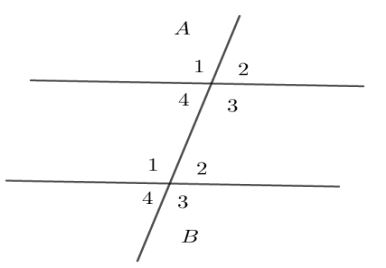
Pada gambar di atas terdapat delapan sudut yang masing-masing diberi nama sudut dengan kode A1, A2, A3, A4, B1, B2, B3, B4, B5.

Beberapa hubungan antar sudut yaitu sebagai berikut.

1. Sudut sehadap

A1 dengan B1, A2 dengan B2, A3 dengan B3, dan A4 dengan B4. Besar dua sudut sehadap adalah sama.

2. Sudut dalam sepihak

A4 dengan B1, A3 dengan B2. Jumlah sudut dalam sepihak adalah 180 derajat.

3. Sudut luar sepihak

A1 dengan A4, A2 dengan B3. Jumlah sudut luar sepihak adalah 180 derajat.

4. Sudut bertolak belakang

A1 dengan A3, A2 dengan A4, B1 dengan B3, dan B2 dengan B4. Besar dua sudut yang bertolak belakang adalah sama.

5. Sudut berpelurus

A1 dengan A2, A3 dengan A4, B1 dengan B2, B3 dengan B4. Jumlah besar sudut yang berpelurus adalah 180 derajat.

6. Sudut dalam berseberangan

A4 dengan B2 dan A3 dengan B1. Besar sudut dalam berseberangan adalah sama.

7. Sudut luar berseberangan

A1 dengan B3 dan A2 dengan B4. Besar sudut luar berseberangan adalah sama.

D. Contoh dan Pembahasan

1. Perhatikan gambar di bawah ini

 

Besar ∠ABD adalah ….

Pembahasan :

Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠ABD dan ∠CBD merupakan sudut saling pelurus, maka:

∠ABD + ∠CBD = 180°

7x° + 5x° = 180°

12x° = 180°

x = 15°

 

∠ABD = 7x°

∠ABD = 7. 15°

∠ABD = 105°

Jadi, besar ∠ABD adalah 105° 

2. Perhatikan gambar di bawah ini

 

 

Nilai y adalah ….

Pembahasan :

Untuk menjawab soal ini Anda harus paham konsep hubungan antarsudut jika dua garis sejajar dipotong oleh garis lain. Dalam hal ini ∠CEF dan ∠EAH merupakan sudut sehadap, maka:

∠EAH = ∠CEF

∠EAH = 102°

∠EAH + ∠BAE = 180° (sudut saling berpelurus)

102°+ 3y = 180°

3y = 180° - 102°

3y = 78°

y = 26°

 

3. Perhatikan gambar di bawah ini

 

 

Besar pelurus sudut SQR adalah ….

Pembahasan :

Perhatian** soal ini merupakan soal jebakan, banyak yang mengira kalau soal tersebut menanyakan ∠SQR padahal yang diminta adalah ∠PQS. Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini∠PQS dan ∠SQR merupakan sudut saling pelurus, maka:

∠PQS + ∠SQR = 180°

(5x)° + (4x+9)° = 180°

9x° + 9 = 180°

9x° = 171°

x° = 19°

 

Pelurus ∠SQR = ∠PQS

Pelurus ∠SQR = (5x)°

Pelurus ∠SQR = (5.19)°

Pelurus ∠SQR = 95° 

 

4. Perhatikan gambar berikut

 

 

Besar sudut nomor 1 adalah 95°, dan besar sudut nomor 2 adalah 110°. Besar sudut nomor 3 adalah ….

Pembahasan :

∠1 = ∠5 = 95° (sudut dalam berseberangan)

 

∠2 + ∠6 = 180° (saling berpelurus)

110° + ∠6 = 180°

∠6 = 70°

 

∠5 + ∠6 + ∠3 = 180°

95° + 70° + ∠3 = 180°

165° + ∠3 = 180°

∠3 = 15° 

 

5. Perhatikan gambar

 

 

Besar ∠BCA adalah ….

∠ABC + ∠CBD = 180° (saling berpelurus)

∠ABC + 112° = 180°

∠ABC = 68°

 

∠BCA + ∠ABC + ∠BAC = 180°

∠BCA + 68° + 42° = 180°

∠BCA + 110 = 180°

∠BCA = 70°