A. Sejarah Teorema Phytagoras
Pythagoras (569-500 SM) lahir dipulau Samos di Yunani, dan melakukan banyak perjalanan melalui Mesir, belajar, antara lain matematika. Pada tahun awal, tidak banyak yang diketahui oleh pythagoras. Ia terkenal setelah mendirikan sebuah kelompok yakni bernama "The Brotherhood of pythagoreans" (persaudaraan ilmu pythagoras). yang mana kelompok ini dikhususkan untuk mempelajari matematika. kelompok ini sangat di kultuskan sebagai simbol, ritual dan do'a. Selain itu, pythagoras percaya bahwa " banyak aturan alam semesta", dan ilmu pythagoras memberikan nilai numerik untuk banyak objek dan gagasan. Nilai-nilai numerik dihubungkan dengan nilai-nilai mistik dan spiritual.
legenda mengatakan bahwa setelah menyelesaikan teorema yang terkenal itu, pythagoras mengorbankan 100 lembu. Meskipun ia sangat diagungkan namun tidak jelas diketahui apakah penulis sebenarnya adalah pythagoras. Para pengkaji dalam kelompok the Brotherhood of pythagoras telah menulis bukti geometris tetapi sulit untuk dipastikan siapa penemu teorema pythagoras itu, sungguh sebuah kelompok yang sangat menjaga rahasia temuan mereka. sayangnya, rahasia tersebut bertantangan dengan ide matematika yang harus diketahui publik. Kelompok the Brotherhood of Pythagoreans telah menemukan bilangan irasional! Jika kita mengambil segitiga siku-siku sama kaki dengan kaki ukuran 1, maka panjang sisi miring adalah. Namun jumlah ini tidak dapat dinyatakan sebagai panjang yang dapat diukur dengan penggaris dibagi menjadi beberapa bagian pecahan, dan ini sangat mengganggu Kelompok Pythagoras, yang terlanjur percaya bahwa “Semua adalah angka.” Mereka menyebutnya angka-angka “alogon,” yang berarti “unutterable.” Akhirnya mereka sangat terkejut dengan angka-angka ini, sehingga mereka dihukum mati seorang anggota yang berani menyebutkan keberadaan mereka kepada publik. Barulah 200 tahun kemudian, yaitu oleh Eudoxus, seorang matematikawan Yunani yang dapat mengembangkan sebuah cara untuk berurusan dengan angka-angka unutterable tersebut.
Setelah ditemukan oleh Kelompok Pythagoras, namun menolak untuk mengakui keberadaan, yaitu bilangan irasional. Dimulailah pencarian tentang bilangan tersebut. Dalah satunya adalah dengan cara berikut. Dimulai dengan segitiga siku-siku sama kaki dengan kaki panjang 1, kita dapat membangun segitiga siku-siku di sampingnya yang hypotenuses panjangnya adalahB. Pengertian Teorema Pythagorasdan seterusnya. Konstruksi ini sering disebut sebagai Square Root Spiral.
Teorema pythagoras adalah suatu aturan matematika yang dapat digunakan untuk menentukan panjang salah satu sisi dari sbuah segitiga siku-siku. Yang perlu di ingat dari teorema ini adalah hanya berlaku untuk segitiga siku-siku, tidak bisa digunakan untuk menentukan sisi dari sebuah segitiga lain yang tidak berbentuk siku-siku.C. Rumus Pythagoras
D. Teorema Pythagoras
E. Pembuktian Teorema Pythagoras
Ada banyak buti yang menunjukkan kebenaran Teorema Pythagoras . Beberapa diantaranya adalah bukti pythagoras yang dikemukakan oleh Pythagoras, Bhaskara, Garfield dan Euclid.
Berikut ini beberapa pembuktian dari teorema pythagoras :
- Bukti dari sekolah phytagoras
- Bukti dari Bhaskara
Bukti berikut ini pertama kali terdapat pada karya Bhaskara (matematikawan India sekitar abad X). Bangun ABCD di bawah ini berupa bujur sangkar dengan panjang sisi c. Di dalamnya dibuat empat buah segitiga siku-siku dengan panjang sisi a dan b.
Luas PQRS + 4 x Luas ABQ = Luas ABCD
- Bukti Euclide
DBQE = NLBD …… kedua bangun kongruen
= MLBC …... alas sama BL dengan tinggi tetap BD
= SRBC ….... alas sama BC dengan tinggi tetap BR
= 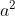
ADEP = KNDA ……... kedua bangun kongruen
= KMCA ……... alas sama AK dengan tinggi tetap AD
= UTCA ……... alas sama AC dengan tinggi tetap AU
= b2
c2 = DBQE + ADEP
c2 = a2 + b2 (terbukti)




Tidak ada komentar:
Posting Komentar