Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran, sedangkan jarak titik terhadap pusat lingkaran disebut jari-jari lingkaran.
Gambar dibawah ini menunjukkan lingkaran dengan pusat P dan jari-jari r.
B. Unsur – Unsur Yang Ada di Dalam Lingkaran
1. Jari-jari Lingkaran
Jari – jari dalam lingkaran merupakan suatu garis yang menghubungkan antara titik pusat dengan titik pada keliling lingkaran.
Pada gambar di atas, jari – jari lingkaran berada pada garis OC, OD, OB dan juga OA.
2. Titik Pusat Lingkaran
Titik pusat yang terdapat dalam lingkaran merupakan suatu titik yang berada tepat ditengah – tengah lingkaran.
Pada gambar lingkaran di atas, titik pusat lingkaran terletak di huruf O.
3. Busur Lingkaran
Yang dimaksud dari busur pada lingkaran yaitu suatu garis lengkung yang di mana adalah bagian dari keliling lingkaran.
Busur pada lingkarang terbagi menjadi dua macam, antara lain: busur besar dan busur kecil.
Disebut sebagai busur besar apabila panjangnya lebih dari setengah lingkaran.
Sementara disebut sebagai busur kecil apabila panjangnya kurang dari setengah lingkaran. Pada gambar di atas, busur lingkarang berada di garis lengkung AC, CB, BD, dan juga AD.
4. Diameter Lingkaran
Yang disebut sebagai diameter pada lingkaran yaitu suatu panjang garis lurus yang mengaitkan antara dua titik pada keliling lingkaran yang melewati titik pusat lingkaran.
Dari definisi tersebut, maka dapat kita ambil kesimpulannya jika jari – jari lingkaran mempunyai nilai setengah dari diameter atau diameter mempunyai nilai dua kali dari jari – jari.
Sehingga rumus yang ditulis yaitu d = 2r.
Pada gambar di atas, diameter lingkaran atau garis tengah lingkaran berada tepat di garis AB dan CD.
5. Tembereng Lingkaran
Pengertian dari tembereng pada lingkaran yaitu daerah yang terletak di dalam lingkaran yang telah dibatasi oleh busur lingkaran serta tali busur lingkaran.
Pada gambar di atas, tembereng lingkarang telah dibatasi oleh busur AD dan juga tali busur AD.
6. Tali Busur Lingkaran
Yang dimaksud dari tali busur pada lingkaran yaitu garis lurus yang mengaitkan dua titik pada keliling lingkaran serta tidak melewati titik pusat lingkaran.
Apabila kita ibaratkan, tali busur lingkaran seperti halnya tali yang terdapa pada busur panah.
Pada gambar di atas, tali busur lingkaran berada pada garis AD.
7. Apotema Lingkaran
Unsur selenjutnya ialah Apotema Lingkaran.
Apotema lingkaran merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran.
Garis apotema pada umumnya terletak tegak lurus dengan tali busur.
Pada gambar di atas, garis apotema berada di garis OF.
8. Juring Lingkaran
Yang dimaksud dengan juring pada lingkaran yaitu suatu daerah yang dibatasi oleh dua garis jari – jari serta telah dibatasi oleh sebuah busur lingkarang yang posisinya diapit oleh dua buah jari – jari tersebut.
Juring lingkarang juga terbagai menjadi dua macam. Antara lain: juring kecil dan juring besar.
Pada gambar di atas, daerah juring lingkaran berada di daerah yang diberi warna hijau yakni juring BOC.
9. Sudut Keliling Lingkaran
Unsur lingkaran selanjutnya yaitu sudut keliling.
Pengertian dari sudut keliling pada lingkaran yakni sudut yang terbentuk sebab adanya pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran.
Apabila kita perhatikan pada gambar di atas, tali busur AC serta tali busur BC yang bertemu di titik C serta membentuk sudut keliling ACB.
10. Sudut Pusat Lingkaran
Unsur yang terakhir yaitu sudut pusat.
Sudut pusat adalah sudut yang terbentuk dari perpotongan antara dua buah jari – jari (OA dan OB) pada titik pusat lingkaran.
Pada gambar di atas, sudut pusat yang terbentuk antara titik A, O, serta B yakni <AOB.
C . Persamaan Lingkaran
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari-jari r
Pada lingkaran disamping jari-jari atau r = OP, OQ = x dan PQ = y. Jarak dari O (0, 0) ke P (x, y) adalah.
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari-jari r
Pada lingkaran disamping jari-jari atau r = OP, OQ = x dan PQ = y. Jarak dari O (0, 0) ke P (x, y) adalah.
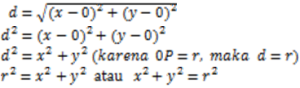
Berdasarkan rumus Pythagoras
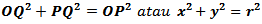
Jadi persamaan lingkaran dengan pusat O (0, 0) dan jari-jari r adalah :
x2 + y2 = r2
x2 + y2 = r2
Contoh :
Tentukan persamaan lingkaran yang berpusat O (0, 0) dan jari-jari 5
Tentukan persamaan lingkaran yang berpusat O (0, 0) dan jari-jari 5
Jawab :
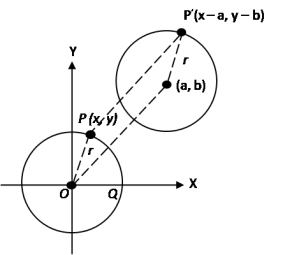
Kita peroleh persamaan.
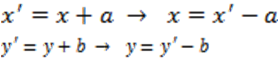
Persamaan lingkaran menjadi (x’– a)2 + (y’ – b)2 = r2
Jadi persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah :
(x- a)2 + (y – b)2 = r2
Jadi persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah :
(x- a)2 + (y – b)2 = r2
Contoh 1 :
Tentukan persamaan lingkaran yang berpusat di (3, 2) dan berjari-jari 4
Tentukan persamaan lingkaran yang berpusat di (3, 2) dan berjari-jari 4
Jawab :
Pusat (3, 2) maka a = 3 dan b = 2.
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
Pusat (3, 2) maka a = 3 dan b = 2.
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 3)2 + (y – 2)2 = 42
(x- 3)2 + (y – 2)2 = 16
Contoh 2 :
Tentukan persamaan lingkaran berpusat di titik P(2, 3) yang melalui Q(5, -1)
Jawab :
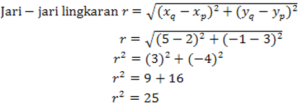
Pusat (2, 3) maka a = 2 dan b = 3
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 2)2 + (y – 3)2 = 25
D. Bentuk umum persamaan lingkaran
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah
(x- a)2 + (y – b)2 = r2
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2+ y2 – 2ax – 2by + a2+ b2– r2 = 0 atau
x2+ y2 + Ax + By + a2+ b2+ C= 0
x2+ y2 + Ax + By + a2+ b2+ C= 0
Jadi bentuk umum persamaan lingkaran :
x2+ y2 + Ax + By + a2+ b2+ C= 0
x2+ y2 + Ax + By + a2+ b2+ C= 0
Contoh :
Tentukan pusat dan jari-jari lingkaran x2+ y2 – 4x +2y – 20= 0
Jawab :
A = -4, B = 2, dan C = -20


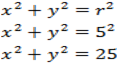
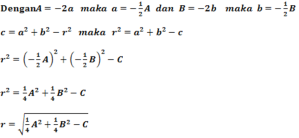

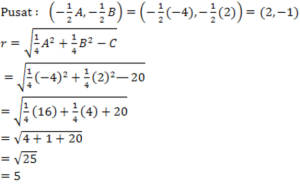
Tidak ada komentar:
Posting Komentar