VIVIN ANGGRAINI HARDI: BARISAN DAN DERET GEOMETRI

A. Pengertian

Barisan Geometri adalah merupakan penjumlahan dari suku-suku dari suatu barisan geometri.

Deret Geometri adalah barisan yang memenuhi sifat hasil bagi sebuah suku dengan suku sebelumnya yang berurutan.

B. Bentuk Umum

Bentuk umum barisan geometri :

Bentuk umum deret geometri :

$a,a\,r^{1},a\,r^{2},...,a\,r^{n-1}$

C. Rumus-Rumus tentang Barisan dan Deret Geometri

Rumus mencari rasio :

Rumus mencari suku ke-n :

Rumus mencari jumlah suku ke-n barisan dan deret geometri :

Rumus suku tengah :

Rumus sisipan :

D. Deret Geometri Tak Hingga

$s_{\infty }={\frac {a}{1-r}}$ untuk -1 < r < 1 di mana $n$ adalah $\infty$ serta $r^{n}$ adalah 0.

Ada dua istilah yang sering dipakai menyangkut barisan atau deret tak hingga, yaitu:

Konvergen

Divergen.

Konvergen adalah memusat atau menuju kepada suatu titik tertentu. Sebaliknya, divergen memiliki arti tidak memusat, bisa jadi menyebar, berisolasi, dan mungkin konstan, yang pasti tak menuju ke suatu titik tertentu.

Pada deret geometri, kekonvergenan bisa dilihat dari rasio deret tersebut.

Deret geometri tak hingga dikatakan konvergen dan memiliki jumlah jika dan hanya jika |r| < 1.

Deret geometri tak hingga dikatakan divergen jika |r| ≥ 1. Deret divergen tidak memiliki jumlah.

E. Deret Geometri ganjil dan genap

$s_{n}={\frac {a}{1-r^{2}}}$ untuk bilangan ganjil

$s_{n}={\frac {a\,r}{1-r^{2}}}$ untuk bilangan genap

F. Sifat - Sifat Deret Geometri

G. Contoh Soal

3. Jumlah 6 suku pertama deret geometri 2 + 6 + 18 + … adalah …

jawaban :

4. Diketahui deret geometri sebagai berikut

3 + 6 + 12 + 24 + ...

a. Tentukan suku ke delapan pada deret tersebut!

b. Tentukan jumlah delapan suku pertama pada deret tersebut!

Jawaban :

5. Diketahui a = 8, r = 1⁄2. Tentukan jumlah deret tak hingga!

jawaban :

VIVIN ANGGRAINI HARDI

Rabu, 15 April 2020

BARISAN DAN DERET GEOMETRI

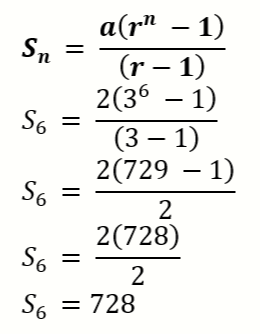
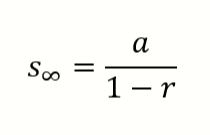
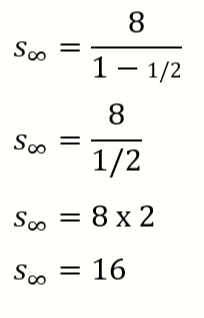
Tidak ada komentar:

Posting Komentar