A. Definisi
Limit adalah batas nilai suatu fungsi f(x) untuk nilai x mendekati a dari kanan (a+) dan kiri (a-).
Limit adalah batas nilai suatu fungsi f(x) untuk nilai x mendekati a dari kanan (a+) dan kiri (a-).
Limit fungsi aljabar adalah menentukan nilai fungsi aljabar jika peubah fungsi tersebut mendekati nilai tertentu.
B. Bentuk Fungsi Aljabar
Terdapat 2 bentuk fungsi aljabar, yaitu :
Bentuk yang pertama :
Bentuk yang kedua :
C. Teorema Limit
Definisi dari limit ini menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu. Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut sebagai epsilon dan delta. Hubungan ke-2 bilangan positif kecil ini terangkum dalam definisi limit.
D. Sifat - Sifat Limit Fungsi Aljabar
Jika n adalah suatu bilangan bulat positif, k konstanta, f dan g merupakan suatu fungsi yang memiliki limit di c, maka beberapa sifat dibawah ini akan berlaku.
E. Cara Penyelesaian Limit Aljabar
- Metode Substitusi
- Metode Pemfaktoran
- Metode mengalikan dengan faktor sekawan
- Contoh soal dengan metode substitusi :
- Contoh soal dengan metode pemfaktoran :
- Contoh soal dengan metode mengalikan dengan faktor sekawan
G. Limit Tak Hingga


H. Contoh Soal dan pembahasan Limit tak tentu
- Contoh soal dengan metode membagi dengan pangkat tertinggi :
- Contoh soal dengan metode mengalikan bentuk sekawan :
- Contoh soal dengan menggunakan rumus





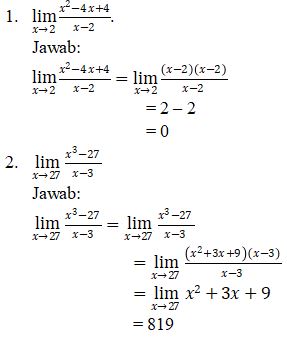



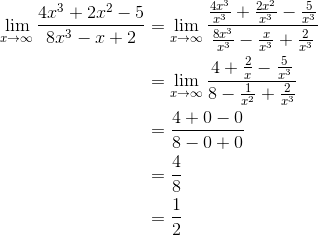
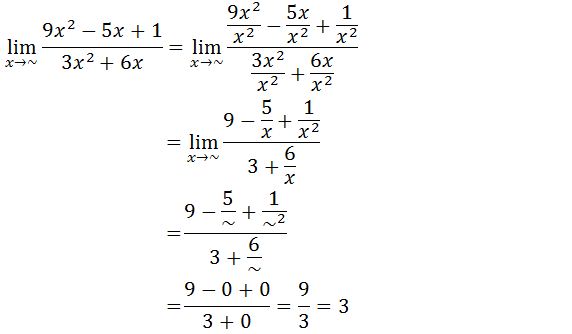

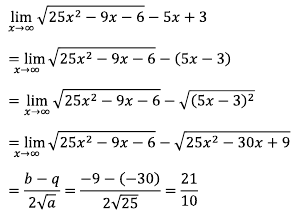
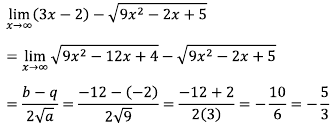
Tidak ada komentar:
Posting Komentar