Persamaan kuadrat
Persamaan kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Bentuk umumnya adalah : ax² + bx + c = 0. Dengan a,b merupakan koefisien dan c adalah konstanta.Persamaan kuadrat dapat diselesaikan dengan beberapa cara, yaitu :
Contoh soal :Persamaan kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Bentuk umumnya adalah : ax² + bx + c = 0. Dengan a,b merupakan koefisien dan c adalah konstanta.Persamaan kuadrat dapat diselesaikan dengan beberapa cara, yaitu :
- Dengan cara memfaktorkan
- Dengan cara melengkapi kuadrat sempurna
- Dengan menggunakan rumus abc
1. tentukan penyelesaian dari :
a. x² + 2x - 15 = 0
b. 2x² + 10x -28 = 0
2. tentukan akar-akar persamaan kuadrat berikut dengan cara melengkapi kuadrat sempurna
x² + 8x - 9 = 0
3. tentukan akar-akar dari persamaan kuadrat x² + 8x + 12 = 0 dengan menggunakan rumus abc
Pembahasan :
1. a. x² + 2x - 15 = 0
apabila dijumlahkan hasilnya +2
apabila dikalikan hasilnya -15
angka nya yang memenuhi 2 ketentuan diatas adalah : 5 dan -3
Sehingga didapatkan :
x² + 2x - 15 = 0
(x + 5) (x - 3) = 0
(x + 5) = 0 dan (x - 3)
x = -5 dan x = 3
jadi, penyelesaiannya adalah -5 dan 3
b. 2x² + 10x -28 = 0
2 ( x² + 5x -14 ) = 0
apabila dijumlahkan hasilnya +5
apabila dikalikan hasilnya -14
angka nya yang memenuhi 2 ketentuan diatas adalah : 7 dan -2
Sehingga didapatkan :
x² + 5x -14 = 0
(x + 7) (x - 2) = 0
(x + 7) = 0 dan (x - 2)
x = -7 dan x = 2
jadi, penyelesaiannya adalah -7 dan 2
2. Carilah angka yang akan di tambahkan terlebih dahulu.
8x ⇢ separuh 8 adalah 4, maka angka yang akan ditambahkan adalah 4² = 16
Sehingga :
x² + 8x -9 = 0
x² + 8x = 9
x² + 8x + 16 = 9 + 16
x² + 8x + 16 = 25
(x + 4)² = 25
(x + 4) = → √25
x + 4 = ± 5
x + 4 = 5 atau x + 4 = -5
x = 1 x = -9
3. x² + 8x + 12 = 0
a = 1, b = 8 dan c = 12
Pembahasan :
1. a. x² + 2x - 15 = 0
apabila dijumlahkan hasilnya +2
apabila dikalikan hasilnya -15
angka nya yang memenuhi 2 ketentuan diatas adalah : 5 dan -3
Sehingga didapatkan :
x² + 2x - 15 = 0
(x + 5) (x - 3) = 0
(x + 5) = 0 dan (x - 3)
x = -5 dan x = 3
jadi, penyelesaiannya adalah -5 dan 3
b. 2x² + 10x -28 = 0
2 ( x² + 5x -14 ) = 0
apabila dijumlahkan hasilnya +5
apabila dikalikan hasilnya -14
angka nya yang memenuhi 2 ketentuan diatas adalah : 7 dan -2
Sehingga didapatkan :
x² + 5x -14 = 0
(x + 7) (x - 2) = 0
(x + 7) = 0 dan (x - 2)
x = -7 dan x = 2
jadi, penyelesaiannya adalah -7 dan 2
2. Carilah angka yang akan di tambahkan terlebih dahulu.
8x ⇢ separuh 8 adalah 4, maka angka yang akan ditambahkan adalah 4² = 16
Sehingga :
x² + 8x -9 = 0
x² + 8x = 9
x² + 8x + 16 = 9 + 16
x² + 8x + 16 = 25
(x + 4)² = 25
(x + 4) = → √25
x + 4 = ± 5
x + 4 = 5 atau x + 4 = -5
x = 1 x = -9
3. x² + 8x + 12 = 0
a = 1, b = 8 dan c = 12
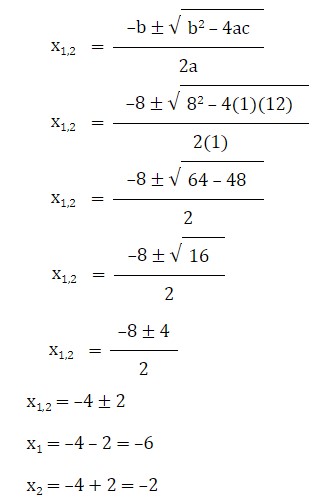
jadi, akar-akarnya adalah x₁= -6 atau x₂ = -2
Tidak ada komentar:
Posting Komentar