VIVIN ANGGRAINI HARDI: PERSAMAAN GARIS LURUS

A. PENGERTIAN

Garis lurus adalah suatu kumpulan titik-titik dengan jumlah tak terhingga serta saling berdampingan. Garis lurus bisa dinyatakan dalam berbagai bentuk persamaan garis lurus, satu garis lurus bisa dinyatakan dalam lebih dari satu persamaan.

Persamaan garis lurus merupakan suatu pemetaan persamaan matematika dalam bidang koordinat cartesius yang membentuk grafik garis lurus.

B. GRADIEN

Gradien merupakan suatu perbandingan komponen y dan juga komponen x , atau yang disebut juga dengan kecondongan sebuah garis. Simbol dari gradien yaitu berupa huruf m.

C. MEMBENTUK PERSAMAAN GARIS LURUS

1.Jika diketahui gradien dan satu titik yang dilalui

Persamaan garis lurus dapat dibuat dengan mengetahui nilai gradien dan salah satu titik yang dilewati $(x_1, y_1)$ . Dalam rumus :

$m = \frac{y - y_1}{x - x_1}$ atau $m(x - x_1) = y - y_1$ .

2. Jika diketahui dua titik yang dilalui

Jika yang diketahui adalah kedua titik $(x_1, y_1)$ dan $(x_2, y_2)$ yang dilewati garis dan gradien, maka rumusnya adalah :

$\frac{x - x_1}{x_2 - x_1} = \frac{y-y_1}{y_2 - y_1}$

D. POSISI ANTARA 2 GARIS

1. GARIS YANG SALING SEJAJAR

Garis sejajar merupakan dua buah garis yang tidak pernah akan memiliki titik potong. Dua buah garis yang saling sejajar ini mempunyai gradien yang sama.

Diketahui gradien garis g = m₁ serta gradien garis h = m₂. Sehingga, hubungan antara gradien 2 buah persamaan garis itu dapat di nyatakan dalam persamaan sebagai berikut:

$m_1 = m_2$

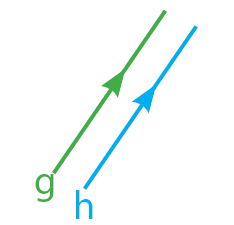
garis g sejajar garis h (g // h)

2. GARIS YANG SALING TEGAK LURUS

Gradien dari dua buah garis yang saling tegak lurus juga mempunyai hubungan. Hubungan dari dua buah garis tersebut di nyatakan jika gradien garis kedua adalah lawan dari kebalikan gradien garis yang pertama. Atau dengan kata lain juga bisa dikatakan jika hasil dari perkalian 2 buah gradien tersebut sama dengan -1.

Diketahui gradien garis g = m₁ serta gradien garis h = m₂ . Sehingga, hubungan antara kedua gradien persamaan garis tersebut di nyatakan dalam persamaan sebagai berikut:

$m_1 * m_2 = -1$

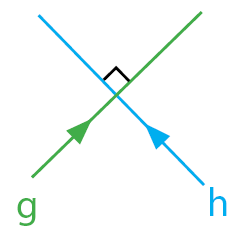
garis g tegak lurus garis h

E. JARAK 2 BUAH TITIK DAN GARIS

Jarak 2 Titik $(x_{1},y_{1})$ dan $(x_{2},y_{2})$

$J = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Jarak Titik dan Garis

Jarak antara garis: $ax+by+c=0$ dan titik $(x_{1},y_{1})$

$J = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}$

F. CONTOH SOAL DAN PEMBAHASAN

1. Diketahui garis lurus melalui titik A (-4, 5) dan B (2, 3). Tentukan nilai dari gradien tersebut.

pembahasan :

2. Tentukan persamaan garis yang melalui titik (2, 3) dan sejajar dengan garis y = 2x – 5

Pembahasan :

3. Sebuah titik P(3, d) terletak pada garis yang melalui titik Q(−2, 10) dan R(1, 1), jika nilai d adala

Pembahasan :

Sebuah titik titik terletak pada sebuah garis maka ketiga titik tersebut memiliki gradien yang sama, sehingga memenuhi rumus di bawah.

$\frac{y_{1} - y_{2}}{x_{1} - x_{2}} = \frac{y_{2} - y_{3}}{x_{2} - x_{3}}$

Titik P(3, d) terletak pada garis yang melalui titik Q(−2, 10) dan R(1, 1), maka :

$\frac{d - 10}{3 - (-2)} = \frac{10 - 1}{-2 - 1}$

$\frac{d - 10}{5} = \frac{9}{-3}$

$-3(d - 10) = 9 \cdot 5$

$-3d + 30 = 45$

$- 3d = 45 - 30$

$-3d = 15$

$d = \frac{15}{-3} = -5$

4. Persamaan garis lurus yang sejajar dengan garis $y = \frac{1}{2}x + 5$ dan melalui titik $P(-1, 2)$

Pembahasan:

Persamaan garis $y = \frac{1}{2}x + 5$ memiliki gradien $m_{1} = \frac{1}{2}$ . Karena persamaan garis baru yang akan dicari sejajar dengan garis $y = \frac{1}{2}x + 5$ maka $m_{2} = m_{1} = \frac{1}{2}$ .

$y - y_{1} = m_{2}{x - x_{1}}$

$y - 2 = \frac{1}{2} \left( x - (-1) \right)$

$2 \left( y - 2 \right) = x + 1$

$2y - 4 = x + 1$

$x - 2y + 5 = 0$

5.Sebidang tanah dengan harga perolehan Rp50.000.000 diperkirakan mengalami tingkat kenaikan konstan Rp200.000 per tahun dalam kurun waktu 5 tahun. Tentukan persamaan garis harga tanah tersebut dan harga tanah setelah 5 tahun!

Pembahasan :

Diasumsikan variabel x sebagai kurun waktu dalam tahun dan y sebagai nilai harga dalam rupiah. Dari soal diketahui bahwa y = Rp50.000.000 jika x = 0. Misalkan gradiennya adalah m maka m = 200.000 (karena tiap tahun bertambah Rp200.000). Sehingga diperoleh persamaan harga sebagai berikut:

untuk x = 5 tahun, maka harga yang diperoleh adalah :